円周率πをモンテカルロ法で求める証明
命題:以下の手順を行った時, 円周率\(\pi\)の近似値は\(\displaystyle\frac{4n_{c}}{n_{s}}\)となる.
- 範囲 \(0 \leq x \leq 1\), \(0 \leq y \leq 1\) の \(xy\)平面にランダムに点を \(n_{s}\) 個プロットする.
- \(xy\)平面の原点から距離が \(1\) 以下の点の個数をカウントし, その個数を \(n_{c}\) とする.
(証明)
\(0 \leq x \leq 1\), \(0 \leq y \leq 1\) を満たす領域の面積を \(S_{s}\), この内部に存在する点の数を \(n_{s}\) とする.
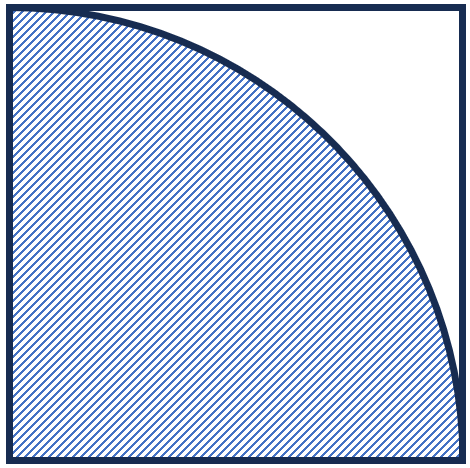
\(x^2 + y^2 \leq 1\) を満たす領域の面積を \(S_{c}\), この内部に存在する点の数を \(n_{c}\) とする. (下図における斜線部)
このとき, \(S_{s} : S_{c} = n_{s} : n_{c}\)
よって, \(S_{c} = S_{s}\displaystyle\frac{n_{c}}{n_{s}}\)
これより円の面積\(S\)は
\(S = 4S_{s}\displaystyle\frac{n_{c}}{n_{s}} = 4\displaystyle\frac{n_{c}}{n_{s}}\) ① ( \(\because S_{s} = 1\) )
また半径 \(1\) の円の面積は積分を用いることにより
\(S = \pi\) ② (証明省略)
①②より
\(\pi = \displaystyle\frac{4n_{c}}{n_{s}}\)
(証明終了)
リンク:モンテカルロ法で円周率を求める